kruskal重构树

听着名字高大上，其实就是 kruskal MST 多加了一步而已。

构建方法

我们还是维持原来跑 kruskal MST 的过程：

• 首先新建 $n$ 个集合，代表图上的每个点，点权都是 $0$。
• 每一次加边会合并两个集合，合并方法是新建一个点，点权为这次加入的边的边权，同时将两个集合的根节点分别设为新建点的左右儿子，然后合并成一个集合，根为新建点。
• 在进行 $n-1$ 轮合并后，我们得到了恰有 $n$ 个叶子的二叉树，同时每个非叶子节点都有两个儿子，这棵树就叫 kruskal 重构树。

这里套用一下 OI-Wiki 的图：

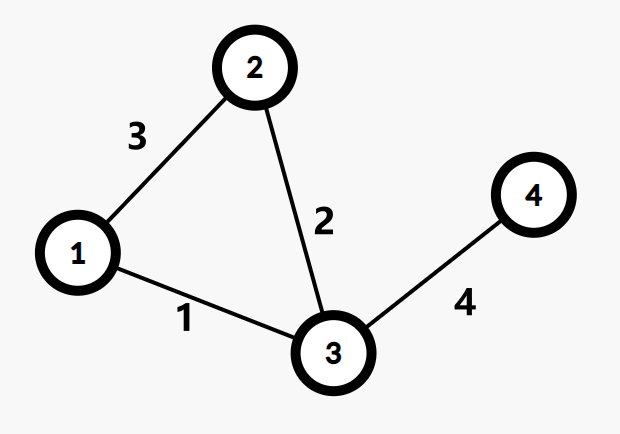
这张图的 kruskal 重构树为:

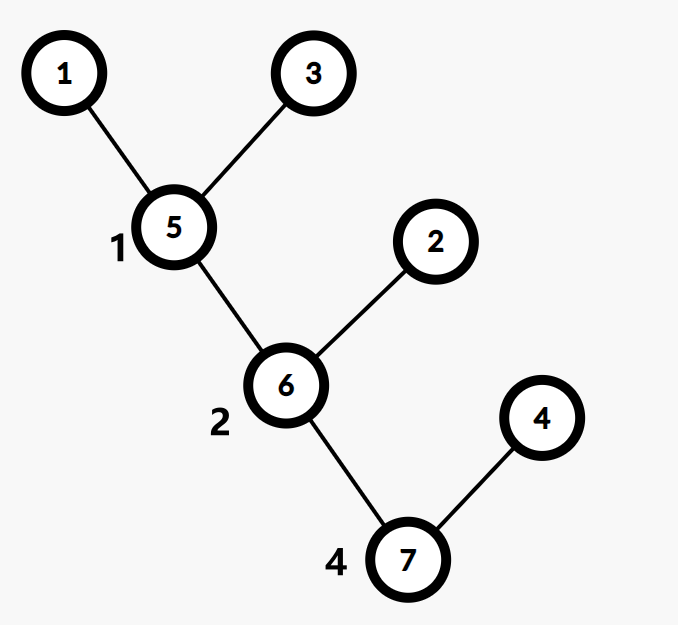
性质

原图中两点之间所有简单路径上最大边权的最小值 = 最小生成树上两个点之间的简单路径上的最大值 = kruskal 重构树上两点间 LCA 的权值。

例题

LOJ137 最小瓶颈路

题目求的就是两点间简单路径上最大边权的最小值，直接敲一个 kruskal 重构树再敲个 LCA 就行了。

NOI2018 归程

首先每条边有两个属性: 长度，海拔；因为这两个属性互不影响，而且家固定在节点 $1$，也就是终点固定，所以我们可以跑一次 dijkstra 处理出 $1$ 号点到每个点的最短路，问题就变成了在开车能到达的点的集合里选择一个最短路最小的。

开车能到达的节点一定都是经过的边的海拔最小值 $>$ 当前海拔的节点，所以我们可以对海拔建一棵最大生成树的 kruskal 重构树，然后从询问的点 $v_0$ 开始向上跳，找到深度最浅的，满足点权 $>$ 当前海拔 $p_0$ 的点，这个点的子树内的点都是 $v_0$ 可以到达的点，然后求子树内最短路的最小值就行了，往上跳的过程可以倍增优化。

当然这题不仅限于这一种做法，也可以用可持久化并查集 $log^2$ 硬草过去这道题，可能可持久化并查集的做法更好想罢。

最短路一定要写 Dijkstra SPFA已经死了

总结

kruskal 重构树其实就是对最小生成树上的每个边新开了一个节点，然后将最小生成树转化成一棵满足堆性质的二叉树，这样很多在最小生成树上对边的询问就会变成重构树上对 LCA 的询问，写起来更加方便而已。